Vamos, ánimo, dije para mis adentros, deja de pensar en la Sabiduría: pide ayuda a la Ciencia.
Umberto Eco (El Péndulo de Foucault).
La vida está llena de decisiones. Algunas se nos presentan más frecuentemente, como dormir o no esos 5 minutos más que me separan de esa versión de mí misma que llega a todos lados con una media de cada color. Otras, como pedirle o no un autógrafo a Capusotto en el chino, no tanto. Unas requieren tiempo de profunda reflexión, otrFIRMAME LA REMERA, DIEGO, TE AMO A VOS Y A TU TATUAJE DE RACIN.
Dentro de las decisiones bien, bien difíciles (esas que te mantienen despierto de noche o en las que pensás cuando estás en la ducha), suelen encontrarse las relacionadas con el amorrrrrr *emoji de corazón*. Y cuando hablo de amor hablo de amor amor, no de amor después de un par de birras y solamente si en casa no terminaron de bajar los torrents. Amor de darle la llave de abajo, de borrar otros números de teléfono, de enredarle los cromosomas en un nene divino que se parezca a los dos.
Pero amor también es ‘¿Y si, en vez de seguir como venimos, nos fijamos si nos estamos perdiendo de algo mejor?’. La pregunta anterior no es poco común y se cimienta en el miedo de que se nos hayan estado escapando oportunidades. Lo que tenemos se define en función de a qué renunciamos para tenerlo, y medio que tan alta es la apuesta que a nadie le gusta jugársela a ciegas.
Tener algo, de alguna forma, es también no tener todo el resto.
Afortunadamente, que sea un monstruo con el que todos nos tropezamos alguna vez significa que es un monstruo con el que se encontraron algunos científicos también. Parece que el primer buen hombre que tuvo ganas de encarar este problema desde la ciencia fue un señor llamado Merrill M. Flood, y lo describió más o menos así:
Supongamos que vas a salir con once bellas personitas, de entre las cuales tenés que elegir una para casarte. No podés salir con varias a la vez ni abandonar a una y volver con otra que saliste antes (es matemática, no la vida, y no, no está bueno, es tu ex y no da seguir con los mensajes). Entonces: ¿Cómo hacés para elegir a la mejor de todas?
Pasaron algunos años, todavía más científicos se encontraron con este problema y se enteraron de que otros también estaban tratando de resolverlo. Lo habían bautizado con el poco progresista nombre de ‘Problema de la Secretaria’ y lo enmarcaban en la posibilidad de encontrar a la mejor persona para un puesto de trabajo haciendo entrevistas secuenciales donde las decisiones no tuvieran vuelta atrás. O sea que sí, se parece bastante a buscar pareja. Después de investigar un rato (soluciones, no secretarias ni parejas) finalmente hallaron una estrategia que, de seguirla, aseguraba que tuvieras las máximas chances de pegarle y casarte con el mejor candidato (sí, casarse es re demodé, pero esto le apunta a la optimización de una conducta dada, no a la generación de una conducta mejor que la que acostumbramos).
Esa estrategia es más o menos la siguiente:
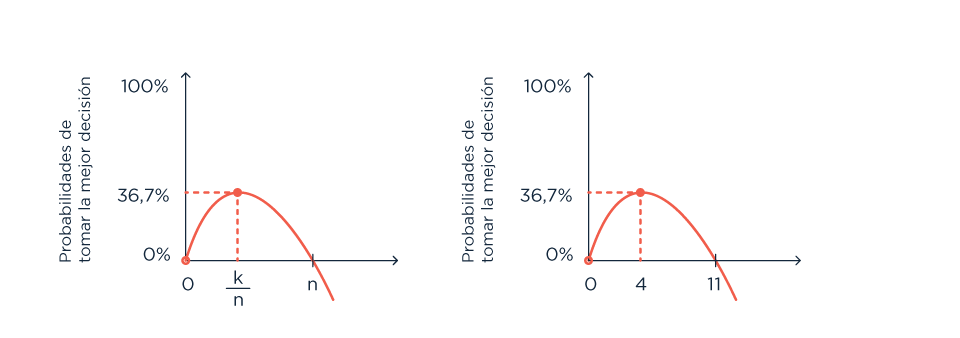
- Salir con los primeros *número total de personas dividido e* (vamos a tomar un número de candidatos de 11 porque hay boooocha de Nemos en el mar, pero el ejemplo lo necesitamos abarcable). Rechazar a esos 11/e. Es decir, 11/2,718… O sea, no volver a llamar a los primeros 4 pretendientes.
- Salir con el siguiente (sería el quinto).
- Si no es mejor que el mejor de los que rechazaste en el paso 1, lo rechazás. Si es mejor, BAM, te aferrás a él (o ella) como a la última birra del desierto.
Supongamos que puntuamos a todas estas personas del 1 al 10 respecto a qué tan buenos esposos/as serían, pero antes supongamos que podemos ponerle puntos a las personas y que eso no escandaliza a nadie; que para políticamente correcto está el bueno de Facundo Arana (NO ABRAN EL LINK ES UNA TRAMPA).
La primera persona con la que salís resulta ser un embole. La rechazás, la puntuás con un 2 y la mandás a tocar el saxo al subte con la esperanza de que no vuelva a hacer un cover de Radiohead nunca más. Con las siguientes dos personas medio que la pasás bien pero no te convencen, entonces las rechazás y las puntuás con un 5 a cada una. La próxima persona es genial, le gusta la misma música, detesta la homeopatía, sería incapaz de tuitear el final de Game of Thrones porque a él sí lo abrazó la mamá de chiquito. Todo fantástico. Pero aunque sea LO MÁS, no podés aceptarla porque está dentro de las primeras cuatro, así que la rechazás pero le ponés un 8.
La quinta persona también es copada, no tanto como la anterior, pero tiene lo suyo. La podés aceptar porque no está dentro de las primeras cuatro, pero la puntuarías con un 7, y el mejor puntaje dentro de los primeros cuatro es un 8, así que la rechazás y le ponés el 7. La próxima persona es realmente lo más más más de la vida y te parece que da ponerle un 9. Como 9 le gana al mejor de los primeros cuatro, que es 8, la aceptás, te casás, viven felices y comen perdices, o capaz milanesas con fritas o sorrentinos con salsa de hongos, que no riman pero son mucho más ricos. Con Facundo Arana te mandás de vez en cuando un whatsapp. Él está muy bien, sigue bueno, se casó y dejó las harinas y los covers.
¿Cómo lograron encontrar esta táctica? Aplicando algunas ideas propias de la teoría de la probabilidad, la rama de la matemática que se usa para estudiar fenómenos aleatorios: cosas azarosas, que no siguen un patrón (como la cara de una moneda que queda a la vista después de que la tiremos al aire y caiga al piso). Particularmente, este problema está relacionado con el concepto de ‘tiempo de espera’: una regla que nos dice cuándo dejar de hacer algo o frenar un proceso en base a lo que pasó antes y/o lo que está pasando ahora. No se vale volver al futuro, y lo mejor es que es aplicable siempre que tengas que elegir algo entre muchos, en orden y sin repetir, y trates de pegarle a algo que esté lo más piola posible, porque todos obedecen a la misma distribución de probabilidades:
La estrategia de la que hablamos tiene dos defectos bastante importantes: el primero es que puede pasar que no aparezca nadie mejor que los primeros que rechazaste y te quedes solo para siempre (lo que sería muy triste para vos pero muy feliz para los gatos que vayas a rescatar de la calle y llevarte a vivir con vos). El otro es que suele ser muy difícil estimar con cuántas personas vas a salir de acá hasta que te cases. Lo bueno es que, como Gato es servicio, agregamos una tablita para que sepas a cuánta gente patear antes de darle la llave de casa al próximo que esté por encima de los rechazados.
| Tiroteos Previstos | Candidatos a descartar antes de enseriarse con el próximo maravilloso |
| 1 | No, posta que no. No es buena idea quedarte con el primer helado que comiste. |
| 5 | 2 |
| 10 | 4 |
| 15 | 6 |
| 20 | 7 |
| ¿Te estás poniendo picante? | |
| 25 | 9 |
| 30 | 11 |
La teoría de la probabilidad tiene chillones de aplicaciones, muchas de ellas para nada alejadas de nuestra vida cotidiana. Aparece cuando jugamos a la quiniela, cuando contratamos un seguro, cuando compramos una rifa o participamos de un sorteo y también cuando hablamos de física, de química y de cualquier otra ciencia experimental. Quizás embarrar la magia de estas actividades le saque algo de emoción a la vida, pero nos ayude a tomar decisiones más inteligentes. También, quizás, no sólo no les saque nada, sino que les agregue la satisfacción del entendimiento, o por lo menos un botón rojo de ‘no soy yo, sos vos, que sos un n menor a mi target de candidatos dividido e’.
NOTA: Como Lau es manija, incluimos una descomposición re piola del Problema de la Secretaria que armó como apéndice de la nota, para el que tenga más hambre de matemática que el resto de los mortales, o tenga interés en planillear mejor sus opciones, lo que pase primero.