En el octavo capítulo de Alicia en el país de las maravillas, el gato de Cheshire desaparece, dejando solamente su sonrisa (o una mueca, depende del traductor). Si buscamos alguna imagen de esa escena (en la película de Disney, por ejemplo, o en los extraordinarios dibujos de John Tenniel) vamos a notar, tal vez, algo curioso: lo que queda del gato no es la sonrisa, sino la boca sonriendo. ¿Se puede dibujar una sonrisa sin dibujar la boca? Parece que no. Pero todos sabemos que, en el fondo, la sonrisa y la boca que sonríe son cosas bien distintas. La sonrisa del gato (dice Martin Gardner) es como la matemática: una abstracción de las cosas que conocemos. Por un lado, es genial, porque nos deja pensar en términos abstractos y generales, evitando las distracciones de lo concreto. Pero, por otra parte, tiene un problema: es bastante poco intuitiva y, cuando tratamos de razonar en esos términos sin mucha formalidad, peligra nuestra cabeza, como la de la propia Alicia. Por lo general no nos importa: no solemos andar por ahí tratando de separar una esfera en otras dos esferas, cada una del mismo volumen de la original, o buscando el punto del mapa que coincide con el lugar en el que el mapa está apoyado. Pero a veces sí. Para casi cualquier actividad (desde hacer un experimento en nuestro laboratorio a poner plata en una apuesta) necesitamos razonamientos estadísticos y, por lo general, los hacemos muy mal. No es que lo diga yo. Hay gente que se tomó el trabajo de llevar a cabo análisis estadísticos para averiguarlo. (¿No es genial construir un microscopio que permite ver en detalle cómo funciona el mismo microscopio? Yo le voy a decir metascopio, principalmente porque suena hermoso). Tenemos falacias estadísticas del mismo modo en que tenemos falacias lógicas y, si no las evitamos, terminamos estando segurísimos de cosas erróneas. Y si pensás que esto no es demasiado importante, pegate una vuelta por la vida de la pobre Sally Clark.
Meine Freundin fiel in eine Senkgrube
Una vez, charlando con un viejo amigo en un bar, mencionó que había notado algo raro en mi vida. Le pregunté qué y me contestó que era extraño que mis últimas tres novias hablaran alemán. No estás particularmente en contacto con alemanes, y no es un idioma popular en Argentina, así que demasiada coincidencia para ser casual, dijo. ¿Nunca les pasó algo parecido? ¿Que el número de patente del auto que se detiene junto a ustedes termine justo como su DNI? ¿Encontrarse, el mismo día y por separado, con dos compañeros de primaria a los que no veían desde que Luca dijo ‘un austral’? Vivimos rodeados de pequeñas, o grandes, coincidencias, de Gachis y Pachis para las que no tenemos una explicación y nuestra reacción automática, como la de mi amigo, es sorprendernos, si son pequeñas, y empezar a pensar en milagros, si son grandes.
Todos de Sagitario
¿Es tan raro como cree mi amigo? En realidad, no. Sería rarísimo que yo eligiera una característica cualquiera, digamos, ser de Sagitario, o medir más de 1,80, y tres personas al azar, y las tres tuvieran esa característica. Pero este no es el caso. Acá lo que pasó es que mi amigo encontró una característica y la notó, porque nos fijamos mucho más en las coincidencias (las tres hablan en alemán) y no en las diferencias entre ellas (casi todo lo demás, por suerte). Si tenemos muchos atributos, y pocas personas, lo raro sería no encontrar una coincidencia.
Para ser más concretos, construyamos algunas novias esféricas y sin rozamiento (contené tu imaginación por un momento, si no te vas a perder el resto de la nota) y usémoslas de ejemplo. Supongamos que cada persona puede definirse por una serie de características binarias (es rubia o no lo es, habla alemán o no, etc.) y que sean independientes entre sí. Es una simplificación –los lectores atentos ya saben que las pelirrojas tienden a ser pecosas, por ejemplo– , pero no importa). Agreguemos además que estas características pueden estar presentes o no con la misma probabilidad (sí, ya sé, otra simplificación, pero no importa para este argumento), y que sólo vemos una coincidencia entre personas si esa característica está presente en todas, no si está ausente. Ahora imaginemos que cada persona tenga solamente una de estas características. ¿Cuál es la chance de que tres personas tomadas al azar coincidan? Es fácil: 1/8, o algo así como el 12.5% de los casos. Y si tuvieran 10 características, ¿cuál es la chance de que tengan una o más en común? Casi el 74%. Y si fueran 100, 99.99%. Casi certeza. Claro que esto depende de muchas otras cosas que hemos simplificado, pero la idea general es la misma: cuantas más características usemos para las personas, más probable es que al menos una de ellas coincida, siempre que el número de personas sea pequeño. Si en vez de tres novias fueran cien, las chances de que todas tuvieran una característica idéntica –en estas condiciones idealizadas– sería básicamente cero, aun si miráramos 100 características distintas (aunque dudo que me quedara energía para recolectar la información).
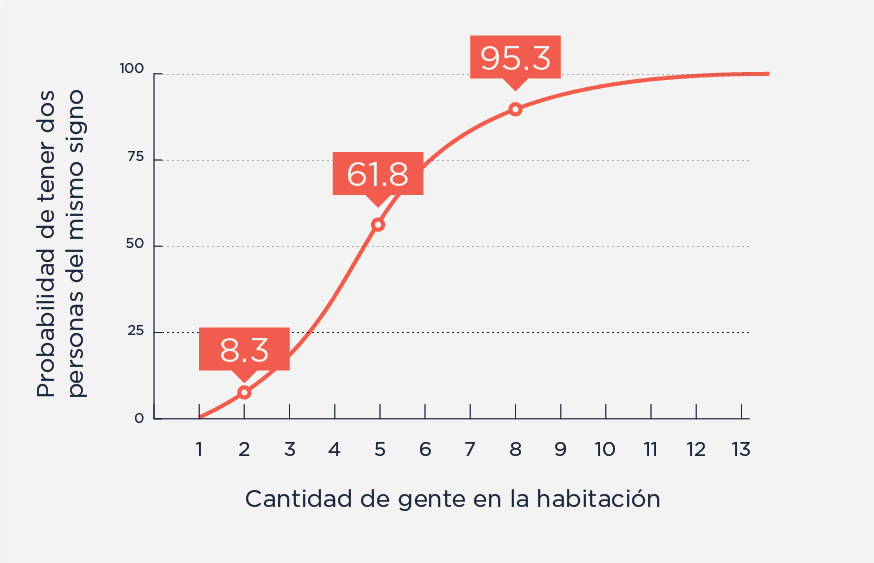
Soy una sigmoidea pequeña y fuerte. Esta es mi asíntota y este es mi pico.
Lo de mi amigo sería sólo una anécdota si no tuviera implicaciones más serias. Por ejemplo, en el año 2003, el gobierno de EE.UU. implementó un programa llamado Total Information Awareness, destinado a registrar y analizar información de todo tipo con el propósito (al menos, con el propósito declarado) de detectar actividades terroristas. Esto tiene un problema serio (olvidémonos de la privacidad, que ya habíamos perdido el día en que nuestro browser nos clavó la primera cookie, o cuando le dimos nuestro DNI a la promotora esa que nos ofrecía no sé qué en el shopping). Supongamos que tengo miles y miles de datos prolijamente guardados de millones y millones de personas. Cuando sospecho que Ramón y Roberto son terroristas, miembros del temible Ejército de la Verdadera Cumbia del Señor, y empiezo a buscarles características en común, dado que tengo tantos datos es casi imposible que no encuentre algo. Es exactamente lo mismo que con las novias germanoparlantes. Pero, igual que antes, es muy probable que eso que haya encontrado no tenga nada que ver con nada. Digamos que descubro que ambos terroristas son hinchas de Colón. ¿Y? ¿Qué hacemos? ¿Empezamos a espiar a todos los hinchas de Colón? ¿Extendemos la vigilancia a otros a los que les gusta el rojo y el negro, como los hinchas de Newell’s, los fanáticos de Stendhal, la ruleta o el Negroni? No sólo dejamos la privacidad tirada en un baldío, sino que tampoco podemos deducir nada útil como resultado. El problema es que tenemos muy pocos terroristas para tantos atributos, y las coincidencias son probablemente sólo coincidencias. Aun si nada tiene que ver con nada, parece que todo tiene que ver con todo.
A menudo vemos patrones en los datos como vemos constelaciones en el cielo, y con el mismo efecto: a veces vemos lo que no hay, y otras no vemos lo que hay.
Un número pequeño, pequeño
Veamos otro caso. Digamos que los equipos A y B van a jugar un partido, y tenemos que decidir por quién apostar. Lo que sabemos es que A y B intentan la misma cantidad de tiros por partido, y que en los últimos 100 partidos A metió, en promedio, el 30% de los que tiró, y B apenas el 20%. ¿Cómo apostamos? La intuición nos dice que va a ganar A. Y, en cierto sentido, es cierto. Si jugaran un partido infinitamente largo, A ganaría. ¿Un poco mucho? Ok, si jugaran muchos partidos lo suficientemente largos, A ganaría casi siempre. Esto tiene, en estadística, el pomposo nombre de Ley de los Grandes Números: si tomamos una muestra lo suficientemente grande, sus resultados serán casi idénticos a los de la población en general (Sí, ya sé. Hice trampa. No definí suficientemente ni casi. Se puede hacer, pero es un poco técnico).
Pero todavía no dijimos a qué juegan A y B. Supongamos que juegan en la NBA. Podríamos derivar formalmente cuál es la chance de B de ganar, o podemos escribir un pequeño simulador en nuestra computadora (es lo que hice yo, que soy vago) y ver que B ganará más o menos el 5% de los partidos que se jueguen. O sea, podemos apostar por B siempre que la apuesta pague un poco más que 20 a 1.
¿Qué pasa si cambiamos la NBA por la Premier League? ¿Seguirían aceptando apuestas 20 a 1 a favor de B? La intuición dice que sí. Después de todo, la probabilidad de acertar de los equipos sigue siendo la misma. Pero la intuición le erra en este caso más que Higuaín. La chance de que B gane pasó del 5% a cerca del 22%, y la apuesta se fue más o menos a 4 a 1. Pero, ¿cómo?, ¿la Ley de los Grandes Números es como la Ley del Offside?, ¿la aplica el árbitro cuando le parece? No, el problema no es ese. Resulta que los números no son lo suficientemente grandes (por algo no definí suficientemente antes, para hacerlos entrar). Veamos. En un partido de la NBA, cada equipo tira en promedio unas 95 veces (sí, estoy obviando que distintos tiros valen distintos puntajes. Es una NBA esférica y sin rozamiento). En uno de la Premier League, más o menos 11 veces. Y si bien en una secuencia larga tenemos derecho a esperar que el resultado sea cercano al promedio, en una secuencia corta aumenta la probabilidad de que pasen otras cosas. A la creencia de que la Ley de los Grandes Números vale también para números pequeños, Kahneman y Tversky la bautizaron irónicamente la Ley de los Pequeños Números. Hicieron un experimento muy elegante, y mostraron que no sólo personas comunes sino también científicos experimentales caen en ese error cuando confían en su intuición. Entendían perfectamente bien las ecuaciones pero fueron, por lo general, incapaces de tener la intuición correcta acerca de qué pasa con las conclusiones cuando usamos el número equivocado de muestras. Algo así como que si sos un perro jugando a algo, cuanto más breve el partido, mejor (también conocido como Teorema de la Brevedad Canina o Modelo de Higuaín).
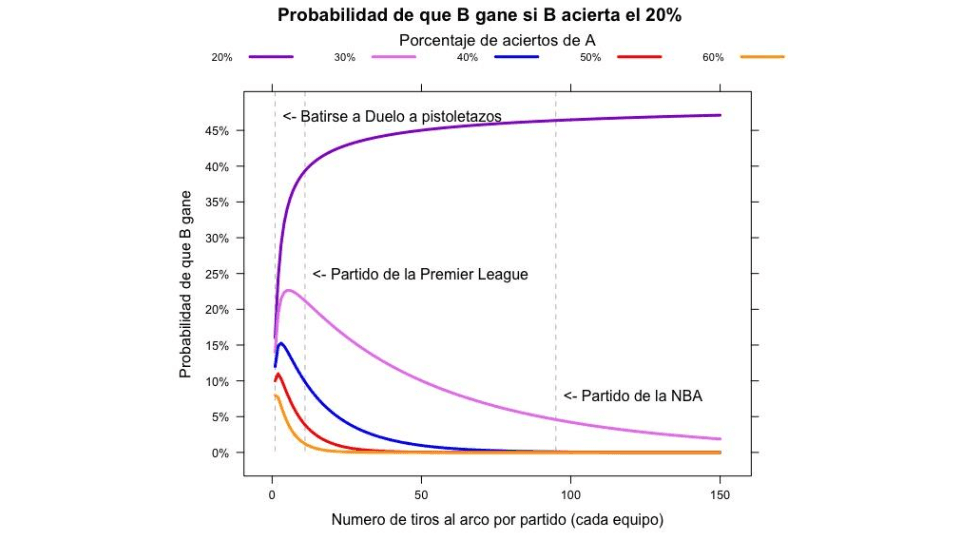
Tirate un qué? Tirate un triple
Espíritus en un mundo probabilístico
Muchos de los descubrimientos sobre nuestra incapacidad de pensar en término de azar (y por lo tanto, estadísticamente) provienen de una escuela de psicólogos cognitivos, liderada por Kahneman y Tversky, que se enfocó en entender los procesos por los que tomamos decisiones (y en el camino demolió la teoría clásica, fundada nada menos que por uno de los monstruos sagrados de la ciencia del siglo XX, John Von Neumann. Ciencia 1 – Argumentos de Autoridad 0). La teoría y los resultados son muchos y muy interesantes, y le valieron a Kahneman el Nobel de Economía. Por ejemplo, hay uno genial que muestra que los jugadores de basket, y los aficionados, tienen una fuerte creencia en las rachas, y que se puede mostrar estadísticamente que no existen. (El premio Nobel de Física y fanático del baseball Ed Purcell mostró que en toda la historia de la MLB hubo una sola racha fuera de escala: los 56 partidos consecutivos bateando de Joe Di Maggio en 1941. Evidentemente, un tipo con suerte, que no sólo hizo este récord increíble sino que también se casó con Marilyn Monroe y aparece en una novela de Hemingway. Crack, que le dicen).
Estos ejemplos, que no son los únicos, muestran que no tenemos ninguna intuición acerca de cosas que involucren estadísticas. O sí, una intuición pésima que nace de confundir azar y orden. Para colmo de males, aun si nuestro razonamiento lógico es perfecto, si empezamos con datos erróneos o simplemente insuficientes, vamos a terminar en cualquier parte. O sea, aun cuando estés completamente seguro, agarrá papel y lápiz y hacé las cuentas, incluida la parte de ‘esto me da este número, pero este número está flojo de papeles porque mis datos originales no eran suficientes’.
No vaya a ser cosa de terminar siendo dentista de Cheshire, sacando conclusiones sobre dientes que no están ahí.
PD: Los datos crudos del gráfico acá

