“Sumisión temblorosa a ritos, voluntad sostenida a gritos, voluntad de unas máquinas tenidas por/expresión más alta del amor en un tiempo mecánicamente acariciado”, dice Fogwill por ahí de las máquinas.
Por todos lados, máquinas. Apretás un botón en el ascensor, y te lleva a ese piso. Apretás un botón en la cafetera, y sale un espresso. Apretás un montón de botones y un cilindro de acero a 1200 °C se mueve a gran velocidad hacia el choque que lo convertirá en un tubo. Apretás =1+1<Enter> en tu Excel y aparece 2, y atrás de todo: máquinas. Mecanismos (mecánicos, electrónicos, o como sea que estén implementados) que toman un input (información, materia, energía, etc.) y lo convierten en un output (vos llegando a otro piso, el café que necesitabas para seguir leyendo esta nota, un tubo, el resultado de una suma). Máquinas. Veloces y, por sobre todo, previsibles: viene un input, sale un output. Siempre igual.
La idea de máquina es la que inspiró a Alan Turing a sistematizar el concepto de algoritmo, de programa, que no es otra cosa que una máquina de procesar datos. Toma un input, lo procesa según unas reglas establecidas, y nos da un resultado. Por ejemplo, hay una máquina de Turing de sumar: le das dos números, te contesta con la suma de esos dos. Pero Turing fue más allá: inventó una Máquina Universal, que toma como input la descripción de cualquier otra máquina de las de Turing y se comporta como se comportaría ésta si la hubiera construido (siguiendo con nuestro ejemplo, toma la descripción de la máquina de Turing de sumar y dos números, y te da la suma de esos dos números como respuesta). La máquina-camaleón, la abuela materna, paterna, antecesor común y Lucy de todas las computadoras que andan y andarán por ahí.
Si la suerte está echada, que se levante porque la vamos a necesitar
En la esquina de enfrente se alza un fantasma que no recorre sólo Europa: lo aleatorio, eso que fluctúa con el azar y se empeña en escapar de la definición de máquina. Sabemos cosas generales de ese fluir, podemos hacer previsiones sobre una población, pero no podemos decir exactamente qué va a suceder sabiendo lo que sucedió. La relación entre input y output la vemos per speculum in aenigmate. Computación, el Manifiesto, inglés, latín bíblico, todo en un párrafo, ¿qué más podés pedir por este módico precio? ¿Filosofía barata y zapatos de goma? Lo pedís, lo tenés: así como las máquinas describen un tipo de orden, los sistemas aleatorios describen un tipo de desorden. Parecen cosas opuestas, Kaos vs. Control, Variabilidad vs. Presión de Selección. Y, sin embargo, podemos construir algoritmos –o algo así, no sea que me tiren con Wikipedia por la cabeza– que computan a partir de números random. O sea, construir una máquina que se alimenta de aleatoriedad. Como crear orden a partir del caos (o casi, aclaro, antes de que una horda de físicos y teólogos me muela a palos por hereje). Bienvenidos al mundo de los algoritmos randomizados. No, zapatos no hay.
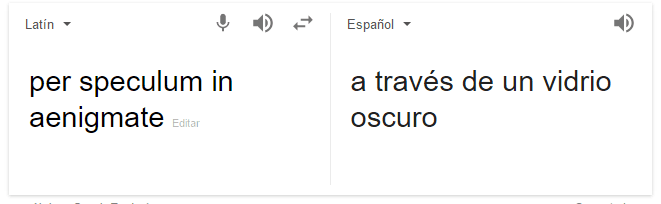
NdR: Obvio que lo tuvimos que googlear. Nosotros tampoco hablamos latín. Pero ¡queda tan bonito! Y capaz que de ahí viene el título de Black Mirror. <3
Blowin’ in the breathalyzer
Imaginemos al pobre Nicolás, con su changuito lleno de bebidas alcohólicas de alta graduación, en una esquina cualquiera de una ciudad dibujada sobre una hoja perfectamente cuadriculada.

Está apurado para llegar a su habitación y beberse el changuito entero. Sabe que va a tomar en el camino, pero no sabe qué camino debe tomar porque, bueno, digamos que el changuito no fue la primera parada del aditivado cognitivo. Lo único que recuerda es que su casa está en una esquina exactamente n cuadras al sur y n al este de su posición actual. ¿Puede hacer algo para llegar? Por supuesto que sí. Lo único que importa es tomar n calles al sur y n calles al este, en cualquier orden. Así que en cada esquina tira una moneda para doblar o seguir derecho (hasta que se le acaben las calles en una dirección, después sólo tiene que seguir en la otra dirección hasta llegar). ¿Cuántos caminos puede recorrer el hombre antes de que podamos decir que llegó a casa? La respuesta la puede calcular hasta un Nobel de Literatura (es el famoso triángulo de Pascal), pero lo que importa acá es que estamos seguros de que llegará a casa, aunque no sabemos exactamente cuánto tardará: algunas cuadras son cuesta arriba o tienen baches, otras son cuesta abajo y se recorren más rápido. Esto no es menor porque, en este tipo de algoritmos, lo aleatorio es el tiempo que tardan en terminar.
El algoritmo es randomizado porque la decisión de cómo elegir el camino se toma al azar. Este tipo de algoritmo randomizado se llama Algoritmo de Las Vegas. Termina siempre, y siempre con la respuesta correcta, pero no sabemos cuánto va a tardar en terminar, ni qué camino tomará.
¿Por qué querríamos usar este algoritmo? Primero, porque es barato de implementar: sólo necesito una moneda y saber la distancia y la dirección a casa. Pero hay más: como las decisiones son todas aleatorias, es imposible predecir por dónde irá Nicolás cada noche. Aun si alimentamos todos los caminos que Nicolás recorrió en el pasado al sesudo algoritmo de inteligencia artificial, no va a acertar más a menudo que eligiendo al azar. Resulta que el azar es una buena forma de ganarle −tal vez− a la información y la inteligencia de los otros (si son mayores que las nuestras, claro). Por otra parte, si en vez de un Nicolás tuviéramos mil Nicolases (o millones de usuarios de Waze, o cientos de programas idénticos tratando de vender acciones idénticas en el mercado, ponele) la randomización garantiza que la congestión será mínima (minga: garantiza que la probabilidad de congestión será mínima).
Por supuesto, si Nicolás tomó aún más que de costumbre, podemos hacerlo todavía más simple. Con un par de restricciones, podemos permitirle que, en vez de avanzar siempre hasta casa, vague al azar, en cualquier dirección, siempre dentro de la cuadrícula, y se detenga recién cuando llegue a casa. Podemos garantizar que llegará con probabilidad 1 (aunque va a tardar muchísimo más: en general tiene que recorrer una cantidad de cuadras proporcional al cuadrado de la distancia de la que partió).
La princesa está triste
Pasemos −sin solución de continuidad− del pecaminoso desierto de Las Vegas al prístino palacio en el que la princesa Graciela Patricia se aburre soberanamente, como corresponde, mientras mira el mar azul que asoma tras una ventana discreta (Spoiler Alert: ya no sale a trepar paredes para robar valiosas joyas. Esos días quedaron atrás). Así que decide aprovechar sus noches reales para calcular el valor de π. Sí, no es muy divertido, pero ¿quién dijo que las princesas se divierten?
Toma del tesoro del palacio un cuadrado, al que llama K, de 2×2, y dibuja adentro del cuadrado un círculo C de radio 1 (hay una sola manera de meter un círculo justo justo en un cuadrado)
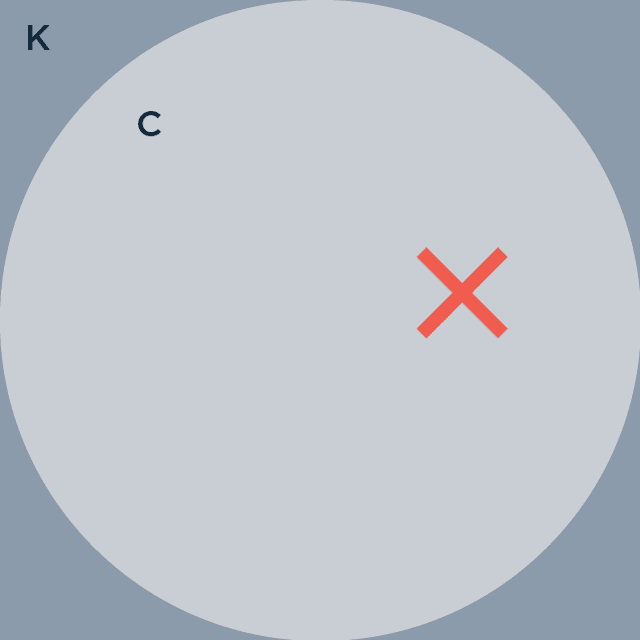
TP 1: Tirarle cosas a un papel y dejar que el azar nos guíe hasta π. La X marca el lugar de nuestro primer dardo hipotético o fideo munición no hipotético.
Ahora empieza a tirar con los ojos cerrados dardos perfectos (de esos que tienen las princesas pero vos no) que siempre caen en K, pero al azar. Algunos de esos dardos caen en C, y otros no.
Ahora, la astuta princesa suma un punto por cada dardo que cayó en C, y cero por cada uno que cayó en K pero no en C. Si la princesa divide la suma de los aciertos en C por el total de dardos que tiró, o sea, calcula cuántos puntos promedio hizo por tiro, ¿cuánto creen que le dará? La probabilidad de caer en C viene a ser el cociente entre la superficie de C y la de K. La superficie de K es fácil, 2×2=4. La de C (recuerden la primaria, o créanle, después de todo es princesa) es π. Mágicamente (o no), si dividimos la superficie de C por K da π/4. Si tiramos n dardos sumamos 1 punto n * π/4 veces en promedio. O sea, que la suma nos va a dar cerca de n * π/4 . Si lo dividimos por n nos da aproximadamente π/4. Es decir, alcanza con multiplicar el promedio de puntos que hicimos por 4 para obtener un número bastante cercano a π.
¿Eh? ¿Acabamos de obtener una de las constantes fundamentales de la matemática tirando dardos? No del todo. Si no le pegamos nunca a C, nos va a dar que π vale 0. Si embocamos todos los tiros, nos va a dar que π vale 4. Pero si jugamos lo suficiente, y el juego es aleatorio –y medio que estamos corriendo el riesgo de intentarlo entre todos y ver qué da, o explotar en el intento–, la princesa va a obtener, por lo general, un valor muy cercano a π. Y puede acercarse a todo lo que ella quiera: cuantos más dardos tire, más improbable es que el número le dé lejos de π.
Y acá quiero hacer un parate, porque todos podemos ser princesas y hacer una versión aproximada del experimento en casa. Dibujen un cuadrado, y adentro del cuadrado un círculo que toque en un único punto los cuatro lados (prueben, hay una sola manera, y el centro del círculo va a coincidir con el del cuadrado). Háganlo como quieran: una cosa genial es que el experimento no depende del tamaño del cuadrado, ni del del círculo, ni del de la princesa (al menos en teoría). Pongan el cuadrado paralelo al piso en una superficie plana. Préndanle una vela a San Cono.
[youtube https://www.youtube.com/watch?v=9rN_-coSjK4]
A continuación voy a calcular el valor de π, porque me place.
Agarren, digamos, 100 fideos munición, o más, y tírenlos al cuadrado con los ojos cerrados. Cuenten cuántos cayeron adentro del cuadrado, y cuántos también adentro del círculo. Repitan 100 veces. O 1000. No va a dar perfecto (algunos fideos se van a ir afuera del cuadrado, capaz que no tiran demasiado al azar, o el cuadrado les quedó inclinado, o algo asi), pero el momento de verlos juntar los fideos va dejarles un recuerdo memorable a los amigos.
Si son desconfiados, antimonárquicos, o gente particularmente visual, no tienen que creer en estas palabras, ni en la de la princesa; pueden jugar ustedes mismos acá.
Esta pausa está insertada para que vuelvan de jugar a calcular π. Qué locura, ¿no?
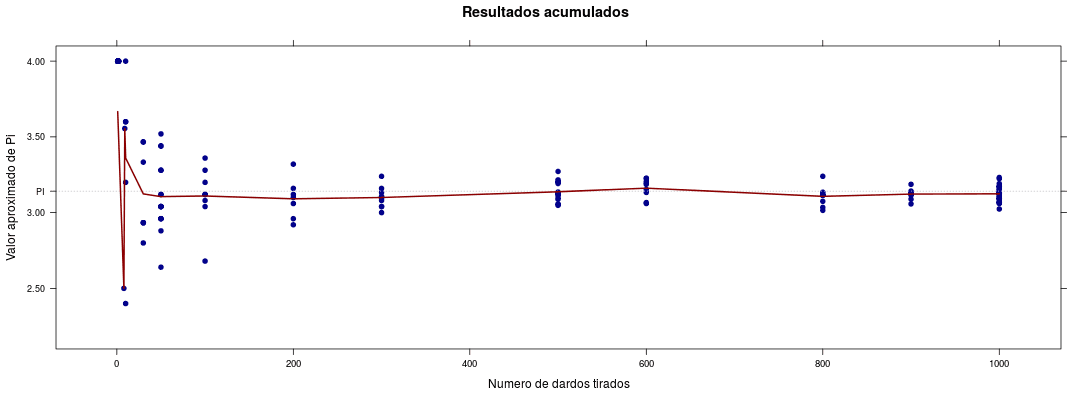
La sugerencia del chef es que elijan múltiples puntos entre 1 y 1000 y tiren varias veces los dados. Todo esto sobre colchón de finas hierbas.
Este tipo de algoritmo, donde lo aleatorio no es el tiempo que se tarda sino el resultado, se llama Algoritmo de Montecarlo. Puede darnos un valor correcto, o no. Pero, usando algunas propiedades estadísticas, si lo corremos suficientes veces, nos podemos aproximar al valor verdadero tanto como queramos. Además, es posible analizar la distribución de sus errores y entender cuán bueno es el resultado que nos da. Por ejemplo, podemos calcular que, si querés estar 90% seguro de que le vas a errar a π por menos del 10%, con unos 1500 tiros te alcanza. Si querés estar 99% seguro, unos 3000 son suficientes. En cambio, si querés estar seguro 90% de que tu error va a ser menor al 0.1%, anda calentando la muñeca, porque vas a necesitar tirar unos 11 millones de dardos.
OK, todo esto sirve para llenar de emoción los atardeceres sosos de la princesa. ¿Sirve para algo más? Sí. Primero, porque acabamos de calcular π tirando cosas sobre un pedazo de papel. SUNALOCURA.
Entre muchos otros ejemplos, hay un problema importantísimo que podemos atacar de esta manera: el de verificar si un número es o no primo (un número natural es primo si tiene exactamente dos divisores: 1 y él mismo). Muchos algoritmos de criptografía (como RSA, que se usa para firmas y certificados digitales, y que está detrás del candadito ese que aparece en el browser y hace que se sientan más seguros cada vez que buscan fotos de gatos o cajas en internet) están basados en elegir números primos. Pero no números pequeños, sino números con muchísimos bits de longitud (cuantos más dígitos binarios, o bits, tenga el número, más difícil de crackear es la clave). Y cuantos más bits tiene un candidato a número primo, más costoso es chequear si es o no primo.
El mejor algoritmo determinístico (o sea, que siempre te da el resultado correcto, una máquina como la gente, digamos) que existe se llama AKS (en realidad se llama Agrawal–Kayal–Saxena primality test, pero nos conocemos desde Cemento), y para testear si un número de n bits es primo, tarda un tiempo que es proporcional a n^6 (n*n*n*n*n*n). No parece tanto, a menos que pienses que testear si un número de 4096 bits es primo o no tarda unos miles de veces más que testear si uno de 1024 bits lo es. Multiplicamos por 4 el número de bits, multiplicamos por miles el costo de testear. Sí, crecer es difícil. No, esto no es una telenovela.
[Nota al margen: qué quiere decir que un número tiene 4096 ó 1024 u otra cantidad cualquiera de bits? Es una referencia a cuántos dígitos binarios se necesitan para escribirlo, cuanta memoria ocupa en la computadora. Pero además, cuán grande es el número. Por ejemplo, un número de 4096 bits tiene más o menos el mismo rango que un número decimal de 1230 dígitos (un millón de números se pueden escribir con 6 dígitos decimales. Así que un número de 1200 dígitos decimales esta cerca de un millon elevado a la doscientos y pico. Uno de 1024 bits, como uno de unos 310 dígitos decimales].
Ahí aparecen los algoritmos randomizados para salvar (¡tal vez!) el día. Porque hay un algoritmo (el de Miller-Rabin) que contesta si un número de n bits es o no primo en un tiempo que es proporcional a n^2 (n*n). Pasamos de n^6 a n^2. Mucho mejor, ¿no? Bueno, no, sí, tal vez, quién sabe. Pero, OBVIO que esa disminución del costo viene con algún temita, y pasa que si el algoritmo dice que el número no es primo, siempre tiene razón, PEEEEEEERO si dice que es primo, hay una probabilidad de ¼ (el 25%) de que se equivoque.
Esto es completamente inaceptable. Cierren ese algoritmo y devuelvanme mi dinero.
Pero la misma aleatoriedad nos tira un centro: como cada corrida del algoritmo de Miller-Rabin es independiente de las demás –toma decisiones al azar en forma independiente–, si corro el algoritmo dos veces, la chance de que se equivoque las dos es de (¼)^2 o 6.25%. Y si lo corro 10 veces, entonces la probabilidad de equivocarse en todas es (¼)^10 , algo así como 1 en un millón. Y si lo corro 20 veces, 1 en un millón de millones. Mejora, ¿no? Y como el costo de cada corrida es n^2, el costo de testear si un número de 4096 bits es primo con probabilidad de error de 1 en un millón de millones es miles de millones de millones de veces más barato que correr AKS. Podés estar bastante seguro por un costo mucho menor, aunque si queres estar absolutamente seguro, es más caro. Como la vida misma, pero con algoritmos. O sea, como la vida misma.
Nace el bit en este mundo
remanyao por el destino
Hay una cantidad enorme de resultados teóricos, y de implementaciones prácticas de algoritmos randomizados, que van desde decidir cómo rutear mensajes en redes hasta machine learning. Y es interesante notar que todo esto proviene de resultados de áreas abstractas de la matemática, de teoría de números, por ejemplo, o de análisis probabilístico de algoritmos. Qué cosa esto de que las ideas geniales y con enorme impacto práctico a veces vengan de lugares imprevisibles, ¿no? Punto para dejar de preguntar para qué sirve lo que hacen los científicos y darse cuenta de que muchas veces lo más valioso es que aún no sabemos para qué sirve.
Este es el punto donde me asalta la duda: ¿lo digo o no lo digo? Es que me da cosa confesarlo. OK, mentí un poco. Dije que iba a mostrar cómo hacer máquinas a partir de aleatoriedad, cómo generar orden a partir del desorden. Después mostré como transformar números aleatorios en valores que caracolean alrededor de π, rutas a casa, números probablemente primos, todo pisteando como un campeón, aparentemente. Pero hay un problema que tal vez alguno haya advertido: todos nuestros algoritmos funcionan usando números aleatorios para tomar sus decisiones, y esa aleatoriedad de algún lado tiene que salir. La pregunta es: ¿de dónde sale? Porque no es lo mismo tirarle fideos a una hoja y contar los que caen adentro y afuera que tratar de pedirle a una computadora que te escupa un número al azar, porque resulta que es totalmente imposible generar bits aleatorios en una computadora (John Von Neumann lo dijo mejor que nadie: “Cualquiera que considere métodos aritméticos para generar números aleatorios está, obviamente, en estado de pecado”. Y antes de que alguien pregunte, todas las computadoras son máquinas de Turing, y todas las máquinas de Turing son métodos aritméticos, pecadoras al parecer).
Acá es clave volver al principio y recordar algo que no vemos tanto como deberíamos: nuestras computadoras son máquinas determinísticas, lo que quiere decir que por definición y a un nivel recontra fundamental no pueden generar números aleatorios. Nos conformamos con generar números pseudo-aleatorios (el término “maomeno aleatorios” no tuvo aceptación en la comunidad matemático-computacional, lamentablemente) para alimentar a nuestros bellos algoritmos sedientos de desorden, y son tan generosos que en la práctica funcionan bien. Bien. Cinco para el peso. Pseudo aleatorio por aleatorio. Computadoras deterministas que arrojan fideos que caen de manera casi casi al azar en el guiso algorítmico, pero nunca tanto. Porque resulta que, computacionalmente, es posible crear orden a partir del caos pero no caos a partir del orden, en un último acto de ironía de un Universo donde la termodinámica se empeña en ir hacia el caos siempre siempre, salvo cuando uno más lo necesita.

