“Hay un concepto que es el corruptor y el desatinador de los otros. No hablo del mal, cuyo limitado ámbito es la ética; hablo del infinito.”
Jorge Luis Borges
Bereishit
Introducción. Nudo. Desenlace. Siempre en orden, patitos en fila yendo de una parte a otra y nosotros siguiéndolos, aun si el fin es apenas otro principio o, como Proserpina descendiendo a los infiernos, el mismo principio. Una escalera por la que vamos cuidando de no confundir el pie con el pie. No importa mucho si es un cuento de Poe, un libro de historia escolar o un artículo sobre ciencia. Un soneto nos manda hacer Violante, y ahí vamos nosotros, midiendo los catorce versos reglamentarios. La alegría de partir, el placer del viaje, la satisfacción de haber llegado.
¿Puedo proponer otra cosa? Porque quiero hablar del infinito y de las cosas extraordinarias hay que hablar de un modo extraordinario. Como en una novela de Patricia Highsmith o una película de Guy Ritchie, quiero poner el final al principio y después, tal vez, compartir los porqué.
Para que el laberinto tenga gracia hay que entrar con los ojos abiertos.
A.
El problema del infinito es antiguo. Por una parte, intuimos con facilidad la idea de que algo no termina. Si tengo un número, siempre puedo sumarle uno y obtener otro mayor. Eso quiere decir que no hay uno que sea mayor que todos los demás. Si la fe es la creencia en lo que no hemos visto, el infinito es algo aún más raro: algo que no hemos visto ni veremos: aunque siempre potencialmente haya uno más para sumar, algún día nos cansaremos de contar o moriremos (nosotros o el Universo). Es más curioso porque ni el tiempo ni el espacio ni la materia parecen ser infinitos, ni siquiera infinitamente divisibles. Un infinito de la mente, que también es finita.
Para muchos, de Aristóteles a Gauss, Kronecker, Poincaré y Wittgenstein, el infinito es algo siempre potencial, no algo que se pueda alcanzar. Que algo sea infinito quiere decir para ellos que el proceso de producirlo puede seguir por siempre, pero nunca podemos considerar el total de lo que el proceso produce (siguiendo con nuestro ejemplo de conteo, podríamos seguir contando para siempre, pero eso no quiere decir que alguna vez vayamos a tener el conjunto de todos los números).
Galileo Galilei nos presenta la siguiente paradoja. Supongamos que tenemos los números naturales (los números de contar, a los que vamos a llamar N para ahorrar espacio)
0,1,2,3,4,5,6,7…
Consideremos ahora el conjunto de los cuadrados de los números naturales (el resultado de multiplicar a cada número por sí mismo):
0,1,4,9,16,25,36,49…
Galileo notó (aunque no fue el primero) que para cada elemento de la primera lista hay uno y sólo uno de la segunda. Cada número de N tiene un único cuadrado. Y cada cuadrado proviene de un único número. Pero eso quiere decir que tengo una correspondencia uno a uno entre ambos conjuntos, el de los cuadrados y el de los naturales. Ahora bien, si tuviera un par de conjuntos finitos (digamos, cowboys y caballos) puedo testear si tienen la misma cantidad de elementos de la siguiente manera: si le doy un caballo a cada cowboy, y no me queda cowboy sin caballo ni caballo sin cowboy, entonces hay la misma cantidad de las dos cosas. Pero eso querría decir que hay la misma cantidad de cuadrados de N que de miembros de N. Parece completamente absurdo: un conjunto que tiene la misma cantidad de elementos que uno de sus subconjuntos. Una matrioska imposible de muñecas que, aun teniendo tamaño idéntico, caben perfectamente una dentro de la otra. Por eso Galileo nos advierte:
Estas son las dificultades que derivan de que pensemos los infinitos con nuestro intelecto finito, dándoles aquellos atributos que les damos a las cosas finitas y acabadas; lo que pienso que es incorrecto.
Para Galileo, el problema es claro: lo finito por un lado, alcanzable por nuestro intelecto finito, lo infinito por otro, algo que no podemos pensar correctamente. Si encontramos paradojas en el infinito, el problema es nuestro, que tratamos de medir la profundidad del océano con un metrónomo.
Z.
Y de pronto, apareció un tal Georg Ferdinand Ludwig Philipp Cantor y nos dio una manera de entender y estructurar los infinitos de la matemática. No sabemos si la idea de infinito le vino a la mente de tanto escribir su nombre completo en el margen de los cuadernos escolares, o en el largo tedio del viaje entre San Petersburgo y Wiesbaden. Sus descubrimientos, que motivaron los ataques de matemáticos (de Kronecker a Poincaré, que lo consideraron un chanta corruptor de la juventud) y la defensa de otros matemáticos (Dedekind, Hilbert, que consideró sus descubrimientos como un paraíso del que nadie podrá echarnos) incluyen lo siguiente:
- Algunos conjuntos que incluyen a los naturales (como los enteros −naturales y sus negativos, a los que llamamos Z− o los racionales −fracciones de enteros, a los que llamamos Q−) tienen exactamente la misma cantidad de elementos que los naturales.
- Los números reales (R) son estrictamente más que los naturales.
- Dado un conjunto cualquiera, llamemoslo A, hay otro conjunto el conjunto de todos los subconjuntos de A, que se llama Partes de A, P(A) o 2A, a gusto del consumidor. Por ejemplo, si A es el conjunto {gato, caja}, P(A) es {{},{gato},{caja},{gato,caja}}. Resulta que P(A) tiene siempre más elementos que A. O sea, no puede haber un último infinito, ni un conjunto de todos los conjuntos (meditando sobre este resultado de Cantor es que el joven Russell demolió la teoría de fundamentos de la aritmética propuesta por Frege. Que su propia teoría haya sido luego demolida por el joven Gödel nos dice con claridad que hay que cuidarse de los jóvenes).
Cantor creía que los infinitos formaban una escalerita. Un infinito, el primero y menor, el de N, al que llamó Aleph cero y otro después, el de R (que además es justo lo mismo que P(N)).
A Cantor le hubiera gustado llamar al infinito de R Aleph uno, en el sentido de que es el primer infinito mayor que Aleph cero, pero de ‘le gustaría’ a que lo pueda hacer hay un montón de comprobaciones. Los matemáticos conocen esta idea de que entre dos Aleph no hay ningún otro infinito por el nombre de Hipótesis del Continuo. Que se llame hipótesis debería ya darnos mala espina, y estaríamos en lo cierto: en 1963 Paul Cohen demostró que es imposible probar o desprobar que entre N y R haya otros infinitos de tamaño intermedio.
Lo más raro que se desprende de esta hipótesis es que nos presenta escenarios bastante poco intuitivos. Podemos decir que sí, que la Hipótesis del Continuo es verdadera, que entre los infinitos de N y R no hay otros infinitos, y nos da una matemática. Podemos decir que no, y nos da otra matemática. Ambas son consistentes (la manera en que los matemáticos dicen que no contienen contradicciones que derrumben todo). Ambas funcionan. Y lo mismo vale para los infinitos mayores que Aleph uno (esto se llama Hipótesis Generalizada del Continuo). Y además, tampoco podemos probar (sin meternos en otro quilombo de axiomas, que es como meterse en una reunión de consorcio) que Aleph cero sea el menor conjunto infinito. No es que hayamos encontrado uno más chico, simplemente no podemos probar que exista sin romper otras cosas.
Tenemos, entonces, una escalera de infinitos cuyo primer escalón no podemos conocer, construida de escalones que conocemos pero que no podemos saber si son los únicos. Curiouser and Curiouser.
Fin del desenlace. Hay infinitos más grandes que otros infinitos. El asesino es Jack el Forastero. Pueden irse. Ahora, si alguno de ustedes ademas de saber qué quiere saber cómo, puede seguir a la próxima sección.
Si, la curiosidad mató al gato, pero peor es lo que le hizo la indiferencia.
Lo que viene a continuación separa a curiosos de muy curiosos, aceptando que el curioso wild-type deja de escarbar cuando la cosa se pone difícil, y el curioso border se alegra de la ocasión de perseguir un agujero de conejo de infinitos. Los infinitos van a dejar de ser así porque son masomenos así, y van a empezar a ser así porque son así, y así, y exactamente así.

En este punto se abren dos caminos. Uno es saltar las siguientes secciones y retomar en la E, aceptar que existen distintos talles de infinito y darlo por entendido. La otra es aventurarse en entender exactamente cómo sabemos eso.
You take the blue pill…
The story ends…
You wake up in your bed and believe whatever you want to believe.
You take the red pill,
you stay in Wonderland.
And I show you how deep the rabbit hole goes.
B.
Digamos que un conjunto es infinito, como notó con cautela Galileo, si se puede poner en correspondencia uno a uno con uno de sus subconjuntos, o sea, si contiene enteramente a un conjunto de su mismo tamaño (más formalmente: si hay una biyección entre él y uno de sus subconjuntos). Está claro que N (el conjunto de los naturales, los de contar) es infinito (en el ejemplo de Galileo hay tantos naturales como cuadrados de naturales). Pendiente todavía está mostrar otros conjuntos que tengan la misma cantidad de elementos que N.
Nuestras computadoras guardan textos codificándolos como bits. Pero esos bits son números binarios. Por lo tanto, usando esa codificación, puedo convertir cualquier texto en un número de N. Por ejemplo, si usamos el código ASCII y le damos tres digitos a cada letra, el texto Oh Tiempo tus pirámides, sería
79104032084105101109112111032116117115032112105114195161109105100101115
Eso quiere decir que no hay más textos que números. Pero como además cada número N puede escribirse como un texto, tampoco hay más números que textos. O sea, hay tantos textos posibles como números en N.
Ahora, puedo pensar que cada función computable es uno o más textos (el de el o los programas que la implementan). Así que no puede haber más funciones computables que números naturales (de hecho, hay la misma cantidad: para cada número puedo escribir un programa que lo computa).
Pero todavía hay más infinitos de exactamente ese tamaño. Pensemos en los números enteros (Z), o sea, los naturales más los negativos. Es obvio que tienen que ser más que los naturales porque los incluyen. Sin embargo, puedo aparearlos así:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | -1 | 1 | -2 | 2 | -3 | 3 | -4 |
Y así siguiendo. Un natural para cada entero. Un entero para cada natural. Un cowboy por caballo. Biyección. La misma cantidad. Desconcierto (o eso espero).
C.
En un sentido, no es tan sorprendente que esto pase. N, Z, los textos, son bastante parecidos entre sí. Por ejemplo, llega un punto que entre dos enteros o dos naturales (o dos textos, si los ordenamos de alguna manera) nunca hay otro en el medio. Son, entonces, discretos. Están bien ordenaditos.
Distinto es el caso de los números racionales, también conocidos como Q, esto es, de los números que se forman como fracciones de números enteros. Por ejemplo ¼ o 9/256 o 1000/(-5). Ahí siempre hay otro entre cualquier par (por ejemplo entre 0 y 1 está ½, entre 0 y ½ está ¼, entre 0 y ¼ esta ⅛, y podríamos seguir así infinitamente como Aquiles cuando se le escapó la tortuga). La intuición nos dice que tiene que haber más elementos en Q que en N. Claro que sí. Y la intuición va a darse derecho de morro contra la pared.
Sí, resulta que hay tantos racionales (Q) como naturales N. Sorprendidos, espero. ¿Confundidos? Claro que sí. Todos los que vimos esto por primera vez nos confundimos.
Pensémoslo así. Primero, podemos formar todos los pares ordenados de números naturales (un conjunto al que llamamos NxN o N^2).
Imaginemos todos los cuadraditos de una hoja de papel cuadriculado infinita donde cada cuadradito tiene como número un par que indica la distancia al cero en la dimensión horizontal, y otro que indica la distancia al cero en la vertical.
Hagamos esto: pongamos a los naturales en una larga tira de papel. Ahora cortamos de esa tira una tirita con un sólo número, [0], después otra con los dos que siguen [1,2], después otra con los tres que siguen [3,4,5], después otra tira con los cuatro que siguen [6,7,8,9] y así siguiendo: en la n-ésima tira hay n números. Podemos disponer la tira sobre las diagonales del papel cuadriculado como sigue (se lee la diagonal que va para allá, y cuando digo ‘para allá’ estoy haciendo un gesto de abajo para arriba, de derecha a izquierda, para allá):

En la primera mini-diagonal (la del par <0,0>) ponemos la primera tira [0]. En la segunda (la del <1,0> y <0,1> ponemos la segunda tira [1,2]. Como la n-ésima mini-diagonal tiene exactamente n lugares, le entra perfectamente la n-ésima tira que cortamos. Así que para cada par <x,y> hay exactamente un natural, y viceversa (si quieren mirarlo más formalmente, la función que estamos calculando es f(x,y) = ½ (x+y)(x+y+1)+y. Se puede probar que es biyectiva).
No puede haber más elementos en Q (las fracciones) que en NxN (el cuadrado donde las fracciones se representan con números naturales arriba y abajo). ¿Por qué? Porque cualquier par de números es una fracción*.
N, entonces, tiene tantos elementos como NxN (y entonces, como Q esta hecho un sandwich entre N y NxN, tiene que tener la misma cantidad de elementos que ambos).
Tranquila, intuición. Va a estar todo bien. Todo, todito. Menos vos.
D.
Ok. Calmémonos. Tal vez no es para tanto. Tenemos un infinito, el de N, y un montón de otros conjuntos (Z, Q, los textos, las funciones computables) que tienen la misma cantidad de elementos. O sea, capaz que tenemos un solo infinito, y nada de esto tiene ninguna importancia. Por un lado, las cosas finitas. Por otro, las infinitas. Galileo Reloaded.
Volviendo a éste mismo, su reflexión sobre los infinitos viene de algo que notó acerca de los número reales −R, todos los que hay en una recta−, y que sabía cualquier pintor del Renacimiento: que siempre es posible proyectar un segmento sobre otro de distinto tamaño.
Es lo que se hace cuando se pinta en perspectiva, ¿no? Si pinto un objeto en un plano y quiero moverlo hacia un plano que está más atrás, puedo proyectarlo punto a punto en la dirección de la línea de fuga y obtener el mismo objeto, sólo que más pequeño. De nuevo, lo que llamamos una biyección.

Con esto, sabemos que cualquier segmento de R tiene la misma cantidad de elementos que cualquier otro segmento de R.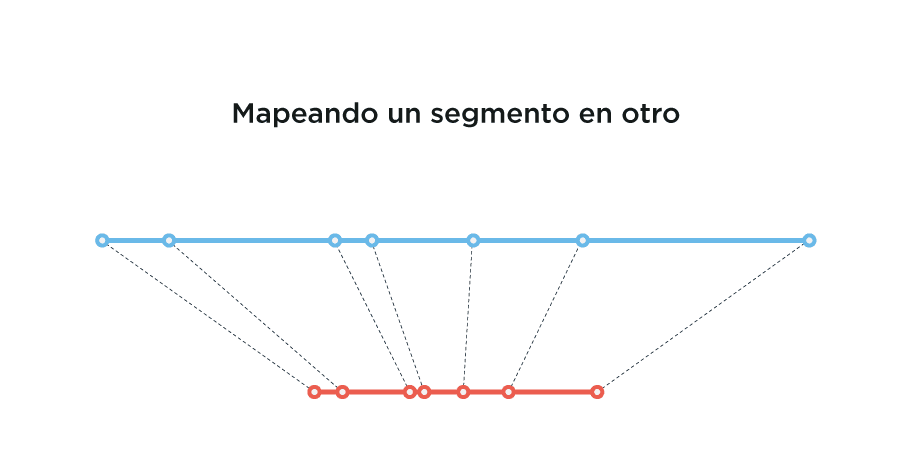
¿Será posible meter todo R en un segmento de R? Suena descabellado, pero resulta que sí se puede. Por ejemplo, la función f(x)=-log(1/x-1) es una biyección entre R y el segmento (0,1) (todos los números reales mayores que cero y menores que uno).
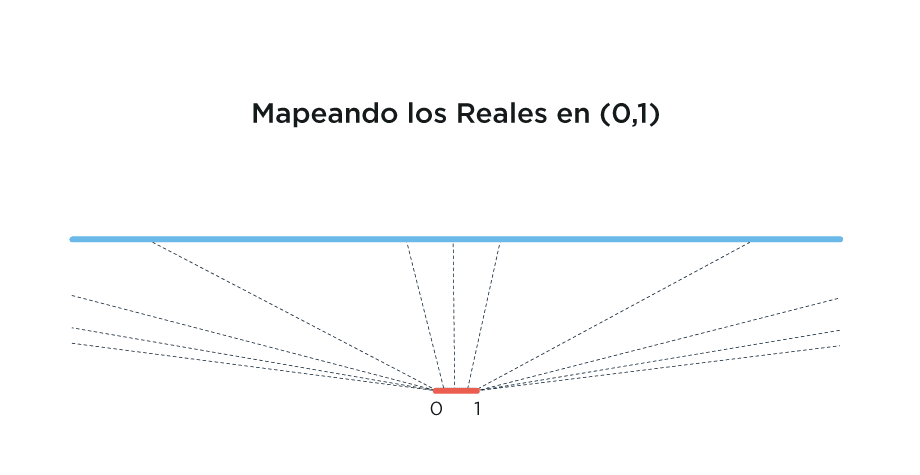
Fue usando una idea como esta que Cantor probó que es imposible armar una biyección (un caballo por cowboy, un cowboy por caballo) entre N y R.
Para que esto no sea solamente promesa, necesito mostrar una prueba (elijo una esencialmente idéntica a la de Cantor) de que no puede haber una biyección entre N y (0,1). Al mismo tiempo aprovecho que, como (0,1) tiene una biyección con R, es lo mismo usar uno que el otro, ya que tienen la misma cantidad de elementos.
Como los caminos retorcidos a veces son todavía más lindos, vamos a imaginarnos optimistas y a suponer que sí existe esa biyección. De ser así, para cada número natural hay un número entre 0 y 1 con el que tiene una relación única: uno que no comparte con los demás naturales.
Podemos hacer una lista prolija de esa biyección, por ejemplo:
0 ↔ 0, 6 6 7 6 1 5 …
1 ↔ 0, 9 1 5 5 4 7 …
2 ↔ 0, 7 2 0 1 0 9 …
3 ↔ 0, 1 2 4 1 0 0 …
4 ↔ 0, 7 9 9 7 7 4 …
5 ↔ 0, 4 4 0 3 3 3 …
. ↔ . . . . . . . …
. ↔ . . . . . . . …
. ↔ . . . . . . . …
Ahora vamos a fabricarnos un número −al que en un ataque de imaginación vamos a llamar x− de la siguiente manera: como primer dígito, le ponemos uno distinto del primer decimal del primero de la lista, como segundo dígito, uno distinto del segundo del segundo, como tercero, uno distinto del tercero del tercero de la lista, como cuarto, uno distinto del cuarto dígito del cuarto de la lista, y así siguiendo. Por ejemplo, para los que mostramos antes podria ser x = 0,721284…
0 ↔ 0, 6 6 7 6 1 5 …
1 ↔ 0, 9 1 5 5 4 7 …
2 ↔ 0, 7 2 0 1 0 9 …
3 ↔ 0, 1 2 4 1 0 0 …
4 ↔ 0, 7 9 9 7 7 4 …
5 ↔ 0, 4 4 0 3 3 3 …
. ↔ . . . . . . . …
. ↔ . . . . . . . …
. ↔ . . . . . . . …
X = 0, 7 2 1 2 8 4 …
Ahora, como x es un número real entre cero y uno, y dijimos que hay una biyección entre esos números y los naturales, x tiene que aparecer en la lista, o sea, tiene que haber un número entero n que corresponda a x. ¿Cuál será? No puede ser el primero de la lista, porque tienen el primer decimal distinto. Tampoco puede ser el segundo, porque tienen el segundo decimal distinto. Ni el tercero. Ni el cuarto. Ni ningún otro: el decimal de la posición n de x es distinto del decimal de la posición n del número que está n en la lista. Entonces x no está en la lista. Pero tiene que estar, si hay una biyección. Por lo tanto, es imposible que haya una biyección entre los naturales y hay estrictamente más números en (0,1) que en N (y que en todos los conjuntos que tienen la misma cantidad de elementos que ellos). Así que hay más reales que naturales. One size does not fit all.
Este tipo de argumento (que en este caso tiene un ligero error, fácilmente salvable, que dejo a ver si alguien lo descubre) es tan famoso que tiene un nombre: Argumento Diagonal de Cantor, y es el argumento usado tanto por Turing como por Gödel para sus resultados más famosos. Muchas veces una idea importante es aún más importante porque abre caminos que otros pueden usar para construir otras ideas aún más importantes.
La intuición está COMPLICADÍSIMA. Por ejemplo, puedo usar esta idea para mostrar que hay un número real que no se puede describir (puedo describir pi diciendo ‘es el número que se obtiene siempre si dividimos la longitud de una circunferencia por su diámetro’; puedo describir raíz de 2 como ‘el número que elevado al cuadrado da dos’). Dar la descripción de un número es, entonces, asociarle un texto. Pero ya vimos que los textos tienen el mismo número de elementos de N (le decimos cardinal de N) , y que no puedo ponerlos en biyección con los reales.
Con lo que hay un número que no puede decir su nombre (otra que Wilde) y (al menos) dos infinitos que no son lo mismo.

Ese momento en el que descubrís que después de atravesar un túnelde caca aparece la sensación de haber entendido uno de los conceptos más fervientemente discutidos de la historia de la matemática.
E.
Podríamos seguir construyendo infinitos, más infinitos, otros infinitos infinitamente.
Rarísimo, pero es así. Y una vez que alguien lo ve, lo ordena, lo comparte, es tan claro que hasta lo podemos explicar en unas pocas páginas, y tan bello como cualquier otra cosa que hayamos hecho. Un laberinto manierista de intuiciones con pies de barro, intuiciones que no son otra cosa que ilusiones equivocadas que, en cuanto desaparecen, dejan ver el paisaje secreto que ocultaban.
Como dijo el mismo Galileo:
…las conclusiones verdaderas, aunque al principio parecen improbables, y apenas se las explica un poco, dejan caer los vestidos que las ocultaban y, desnudas y simples, muestran alegremente sus secretos.
Saludos, curiosos y muy curiosos, audaces que eligieron enfrentar al monstruo y son testigos ahora de infinitos desnudos.
* (hago un poco de trampa: hay fracciones negativas, hay pares de números con un cero abajo que no representan ninguna fracción. No importa, es fácil ver que si los sacamos no pasa nada porque Z tiene la misma cantidad de elementos que N, y si le sacamos el cero a N nos queda la misma cantidad de elementos.)

