Pocas cosas asustan más que recorrer con los ojos el informe del laboratorio que establece tu salud en términos binarios.
Positivos y negativos de tinta pegoteada en papel de hospital que te informan si algo en la suma de lo que elegiste y lo que te pasó se tradujo en una posibilidad, que aún en esa forma potencial, te paraliza.
Nací en los 80, década compartida con el primer caso registrado de paciente con HIV en Argentina –número que treparía hasta decenas de miles para los 2000, la década sin abreviatura instintiva– que me recibía con una pubertad consolidada y una manifiesta voluntad de aparearme, con el abanico de riesgos nuevos (y beneficios potenciales) que eso implicaba.
Cada donación de sangre posterior a mi Sputnik sexual iría acompañada de un doble objetivo: darle una mano a alguien y chequear que estuviera todo en orden, que los tiros venían pasando de costado y que yo seguía siendo un Bruce Willis de férreo sistema inmune (aunque probablemente el orden prioritario estuviera invertido, siempre fui más cagón que altruista).
Cada informe posterior suponía una danza de probabilidades y certezas. La urgencia de ver ‘HIV no reactivo’ impreso regularmente, pero al mismo tiempo la creciente duda respecto de esa seguridad que aparecía a medida que progresaba en la Facultad. Mi forma de ver el mundo iba cambiando, incluidas las ideas de confianza, incertidumbre o potencia estadística. Efectos secundarios, todos, de estudiar ciencia.
En algún momento de esa misma adolescencia, un amigo baterista me dijo que la técnica es lo que conecta el alma del músico con el instrumento. De almas no sé nada de nada, pero la idea de puente me parecía hermosa, más aún cuando descubrí que la estadística era el puente que conectaba los modelos que la ciencia arma para describir el Universo con ese (este) Universo que nos desesperamos por entender.
Cada papelito leído traía consigo enfrentarme a nociones como la sensibilidad o la especificidad de un exámen, palabras no menores porque no entenderlas implica no poder interpretar realmente bien ese resultado.
Una gran mente una vez dijo ‘A la gente le copa que seas científico hasta que le decís que la ciencia le va a dejar más preguntas que respuestas. Ahí te mandan al carajo’. Creo que esto tiene mucho que ver con la falta de respuestas absolutas, de verdades finales y de seguridades completas, y tanto la sensibilidad como la especificidad de una herramienta para hacernos preguntas se estrellan directamente contra la incertidumbre. Contra ese margencito que nos separa permanentemente del 100% de certeza que la ciencia nunca alcanza.
Entender el resultado implica, entonces, saber que la sensibilidad de un ensayo nos dice cuántos casos positivos son, de hecho, identificados como positivos. La buena noticia es que los tests actuales de HIV son muy, muy buenos en términos de sensibilidad, metiéndose en el rango de algo así como el 99,5%. O sea que si tomo a 1000 personas con HIV, el test va a indicar positivo para 995. La mala noticia es para los otros 5, que son margen obligado e incertidumbre en la forma de falso negativo.
Pero todavía no es suficiente, y ahí entra la especificidad, que es la contraparte de la sensibilidad, pero para los negativos. O sea, la proporción de personas NO infectadas que van a ser identificadas como no infectadas. Acá, de nuevo, las buenas y las malas noticias, porque caemos otra vez en los noventaynueves (si vemos varios métodos distintos de diagnóstico, podemos redondear la especificidad de los análisis actuales en masomenos 99.9%). O sea que de cada 1000 personas negativas diagnosticadas, 999 van a ser informadas de ese negativo, pero 1 va a tener un falso positivo.
Todo esto para seguir sin entender cómo leer el resultado, o cómo interpretarlo en un contexto más amplio o más ligado a la realidad individual del que se hace el test porque, aunque tanto la especificidad como la sensibilidad estén asociadas al ensayo; el resultado, no. El resultado está ligado a esos dos valores, pero también al que lee, y ahí es cuando entra Thomas Bayes, un estadístico, filósofo y ministro presbiteriano (?) de principios del siglo XVIII del que sabemos no tanto, y mucho de lo que sabemos es más bien inferencia.
Me topé con el susodicho ya cursando estadística (que para los biólogos se llama Biometría, porque ‘Estadística para Biólogos’ era considerado bullying) y, la verdad, le di poca pelota, limitándome a repetir una fórmula que incluía algo así como la posibilidad de calcular la probabilidad de que algo sea de determinada manera, dado que pasó otra cosa antes. Fue cuestión de aprender la fórmula y aplicarla bien, y listo, todo sin entender la potencia que había detrás.
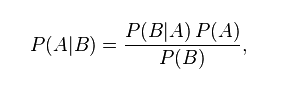
En una fórmula relativamente sencilla, Bayes había encontrado una manera de ponderar qué es ‘evidencia’, y no solamente eso, sino cuánto ‘pesa’ esa evidencia, y lo había presentado de esta forma.
Cosa que no significa absolutamente nada a menos que te pongas a desenredarlo. Esta forma de ponderar modelos, creencias y evidencia dice algo así como que la probabilidad de que una creencia (entendida como modelo que describe la realidad) sea verdadera dada nueva evidencia es igual a la probabilidad de que esa creencia sea verdadera INDEPENDIENTEMENTE de esa evidencia, por la probabilidad de que esa evidencia sea verdad dado el hecho de que la creencia es cierta, dividido por la probabilidad de que la evidencia sea verdad, independientemente de que la creencia sea o no verdad.
Sí, ese párrafo anterior es un garrón, pero garrón con empatía, porque para mí también fue un garrón ordenarlo, escribirlo y que dijese lo que dice la ecuación. A veces no hay forma de simplificar y lo que te queda es volver a leer hasta que se genere ese chispazo donde decís ‘ahhhhhhh’ y te das cuenta de que la tercera lectura valió la pena (aunque, nobleza obliga, creo que en su momento me llevó bastante más de tres lecturas entender qué quería decir Bayes).
Mal y pronto, no nos dice si algo es verdad, pero nos cuenta cómo actualizar nuestra forma de ver el mundo (esa creencia), cada vez que aparece un pedacito de evidencia nueva, sea fortaleciendo ese modelo o debilitándolo.
En este caso, mi primera aproximación a entender cómo leer el análisis parte de entender la especificidad (ahora entendida como probabilidad de dar negativo dado que negativo), la sensibilidad (ahora como probabilidad de dar positivo dado que positivo), y un factor más: la evidencia previa.
Esta idea, la de ‘evidencia previa’, es el gran grano en la cara de Bayes. ¿Cómo nos aseguramos de estar estimando bien las situaciones previas? ¿De dónde sale esa información? ¿Cuánto le creo? Estas y muchas otras preguntas las pueden hacer en un congreso de estadística, porque es el gran tema por el que se están matando hace años y porque no tengo una respuesta. Lo que sé es que, a los fines de este problema, la evidencia previa que voy a usar van a ser los mejores datos poblacionales que tenga disponibles, que me dicen que, en Argentina, el 0,4% de la población total es portadora de HIV (o, en términos que puedo usar en la ecuación, 0,4/100, o 0,004).
Mi probabilidad a posteriori (o sea, después de agarrar la previa y actualizarla según lo que sé de los exámenes y lo que sé de la distribución poblacional total) es algo así como:
Ahora bien, los métodos actuales no tienen nada que ver con los de hace 10 o 15 años, lo que quiere decir que tanto la sensibilidad como la eficacia van a variar con el tiempo*. Pensando en eso y en la angustia del pasado, voy a usar 99% de sensibilidad (o sea que detecta 99 de cada 100 negativos como negativos) y 99% de eficacia (o sea que detecta 99 de cada 100 positivos como positivos).
P(posteriori) = (0.99 * .004) / (0.99 * 0.004 + 0.01 * 0.996)
= 0,00396 / (0,00396 + 0,00996)
= 0,00396 / 0,01392
= 0,2844827586206897
O sea 28%. VEINTIOCHO por ciento.
No el 99 que intuitivamente hubiese respondido si me preguntaban ‘¿Qué significa que el test dé positivo?’, sino un número que no tiene absolutamente nada que ver con mi intuición, y es porque mi intuición, muchas veces, hace las cosas mal.
Aún con métodos mega específicos y mega sensibles, las probabilidades no son lo directas que uno esperaría respecto del ensayo solamente, y ponderar la evidencia previa (en este caso la poblacional), cambia completamente el resultado.
Esto es todavía más sorprendente cuando vemos cómo tanto refinar el método como cambiar la situación previa afecta dramáticamente el resultado. Por un lado, me pregunté qué tan distinto sería el yo de la adolescencia del del presente a la hora de interpretar el mismo resultado, pero esta vez con métodos más sensibles y eficaces. Ahora sí, uso 99.5% de eficacia y 99.9% de sensibilidad.
P(posteriori) = (0.995 * .004) / (0.995 * 0.004 + 0.001 * 0.996)
= 0,00398 / (0,00398 + 0,000996)
= 0,00398 / 0,004976
= 0,7998392282958199
O sea, 80% seguro. 4 de 5.
Lo que implica que mejorar la calidad y certeza de mi toma de datos cambia muchísimo la potencia del análisis.
El otro factor que puede brindarse como definitorio a la hora de analizar el mismo resultado es que cambie la evidencia previa. Yo usé el 0,4% basado en que me incluí de lleno en la población promedio, pero ese dato es relativamente pobre. Si hubiese mejores datos para mi rango de edad, orientación sexual, conducta respecto del uso de drogas o cualquier otra actividad que pudiera definir más acotadamente la población a la que pertenezco y el riesgo asociado al grupo, tendría datos más fiables. Ahí está la pesadilla de la previa, en confiar en esos datos.
Para entender la diferencia, voy a suponer al mismo yo adolescente, con pruebas de 99% eficacia y 99% sensibilidad, pero ahora usuario de drogas inyectables. Esto cambia DRAMÁTICAMENTE la previa, que pasa de ser 0,4% a 6% (ya que 6% de los usuarios de drogas inyectables son portadores de HIV).
P(posteriori) = (0.99 * .06) / (0.99 * 0.06 + 0.01 * 0.94)
= 0,0594 / (0,0594 + 0,00094)
= 0.0594 / 0,06034
= 0,9844216108717269
O sea, 98.4% de probabilidades de que ese resultado positivo implique, en efecto, ser portador.
La pregunta de si poder ajustar la ‘previa’ es una debilidad o, por el contrario, una fortaleza del enfoque bayesiano es todavía otra discusión enardecida. Lo que sí vemos es que esta forma de encarar la evaluación de modelos y evidencia entró de lleno en el corazón de la ciencia de nuestra época, apareciendo como herramienta de análisis pero también como potencial modelo de cómo funcionamos nosotros, de cómo tomamos decisiones, de cómo ajustamos o, por lo menos, de cómo podríamos hacerlo mejor.
En algún lugar del bayesianismo hay un espacio de incertidumbre y de humildad que me atrae. Hay una idea de dejar de negar el sesgo y de tratar de mirarlo, cuantificarlo, atenderlo y, así, empezar a superarlo. Aunque, la verdad, esa evaluación es una sensación personal que nadie debería interpretar como verdad.
Después de todo, puedo estar sesgado.
* (no ajusto la previa poblacional al año 2000, aunque debería, pero es porque necesito mantener el dato fijo para el análisis sobre poblaciones diferentes que viene a continuación)


