La primera vez que vi un grafo me quedé mudo. Era tan contundente y tan intuitivo. Unía la red de amigos de una amiga y colega usando nodos para representar personas y aristas, para mostrar si eran amigos en Facebook. Así como ella veía su mundo representado en una sola imagen, me veía también yo, inmerso en ese mundo y su entretejido social.
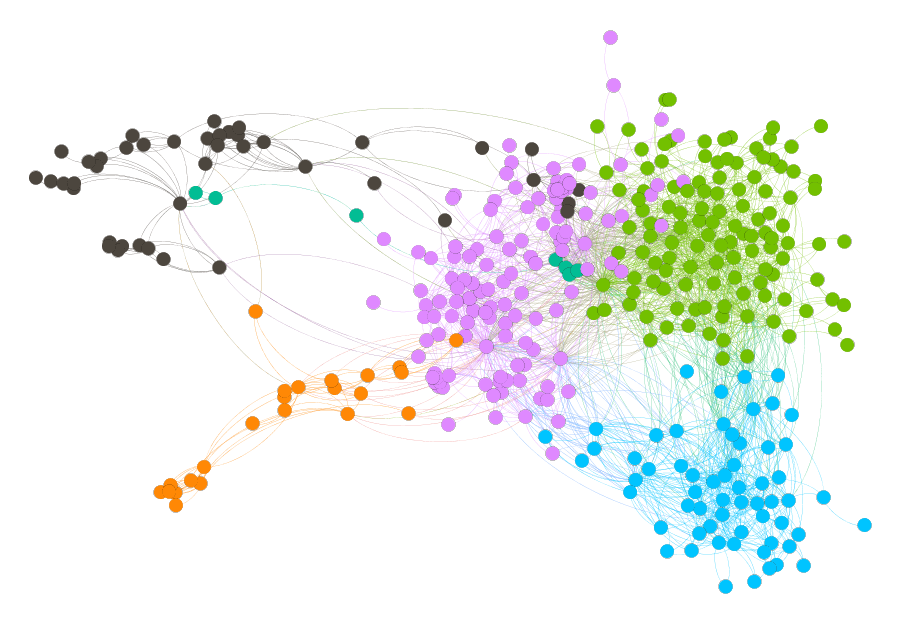
Mi red de amigos de Facebook, con su identidad preservada para que no tengan que hacerse cargo de ser mis amigos. Cada nodo representa a una persona, las aristas aparecen sólo si esas personas son amigas entre sí. De esas interacciones emerge cierto orden. En verde, el clúster más bien Gato: la gente que fui conociendo al hacer esto mismo que hago ahora. En celeste, mi vida universitaria (Exactas <3) , en rosa el clúster más bien diseñoso/periodistoso/proyectista que conocí de redes sociales. El naranja y negro muestran lo poco que se incorporaron mis compañeros de primaria y secundaria (respectivamente) a las otras tres etapas de mi vida.
De ahí para adelante, la obsesión por tratar de adquirir y presentar datos de esa manera se volvió una aventura que, amigos data science mediante, empecé a recorrer, siempre más como aficionado embelesado por la herramienta y sus productos que como científico profesional, pero al mismo tiempo siempre muy atento a la potencia y las distintas aplicaciones que iba sumando esta forma de pensar, procesar y representar información, así como lo permeable que se iba haciendo sobre distintas disciplinas y sobre la resolución de distintos tipos de problemas.
Unos cuantos años después, me di cuenta de que incluso podía ser clave para la resolución de uno de los problemas más grandes de la historia del mundo, uno de esos que todos sufrimos y no una vez, sino muchas, cada vez que llegamos a un encuentro social y nos preguntamos ¿cómo hago para saludar, uno por uno, a todos los presentes, de la manera más eficiente posible?
El camino hasta responder sobre ese trayecto particular tiene, a su vez, uno propio. Podemos empezar por el dato de que un punto verde es Gerry Garbulsky, uno de los organizadores de TEDxRíodelaPlata y el hombre orquesta detrás de Aprender de Grandes, podcast que escucho con regularidad y al que hace un tiempo tuve la oportunidad de conocer también del otro lado, pasando de oyente a entrevistado. Hablamos hora y media. De Gato, de ciencia, de diseño, de la comunidad (y de la idea misma de comunidades en épocas de redes sociales), de Un libro sobre drogas y de políticas públicas basadas en evidencia.
Ya sobre el final de la conversación, Gerry hizo una pregunta terrible. De todas las preguntas en la intersección de ciencia y política pública, él eligió meterse con una dificilísima. No tenía que ver con la regulación de drogas, de eso podíamos contestar con bastante seguridad. No era sobre lo que la ciencia puede aportarle a la discusión sobre interrupción voluntaria del embarazo, no, eso también caía en un terreno que podíamos manejar con relativa competencia. Era una pregunta peor. Gerry quería saber qué podía hacer la ciencia por el tránsito.
Me sentí estudiante enfrente de la bolilla más difícil, y al mismo tiempo como persona que trata de usar una metáfora de bolillas cuando jamás rindió un final con bolilla. Es que la pregunta del tránsito, lejos de ser inocente o sencilla, es una pregunta que me puso de frente a uno de los problemas más hermosos y antipáticos de la matemática, el problema del viajante:
Dada una serie de nodos unidos por una serie de aristas, ¿cuál es la mejor forma de desplazarme para cubrir todos los nodos maximizando el uso de recursos? Soy un cartero que recorre la ciudad para entregar paquetes en cada barrio, una aerolínea tratando de llevar gente a distintos destinos, un mozo tratando de cubrir todas las mesas, pero por sobre todo, soy un problema tremendo de optimización. Problema que se hace evidente cuando notamos la cantidad abrumadora de combinaciones que hay para cubrir todos esos puntos y, por sobre todo, cómo esa cantidad crece a medida que se agregan nodos. Las combinaciones crecen así de rápido porque cada nodo que se agrega es potencialmente un destino u origen nuevo que se recombina con todos los existentes (digamos que crece como (N-1)!/2 rutas posibles para N ciudades, para los amigos (?)). Esto resulta inocentemente en que para 3 ciudades haya un solo recorrido que las une completamente y vuelve al punto de partida, pero para 5 ese número crece a 12, y para 10 ciudades trepa a 181.440 caminos posibles. Ni hablar de unir 30 ciudades, para lo que existen 4*1030 rutas posibles. Una computadora capaz de calcular un millón de rutas por segundo necesitaría 1017 años para resolverlo, lo que significa que si se hubiera comenzado a calcular al comienzo de la creación del Universo (hace unos 13.400 millones de años), todavía no se habría terminado. Todo para unir 30 ciudades de la manera más eficiente posible. MAL PROBLEMA PARA PREGUNTAR, GERRY.
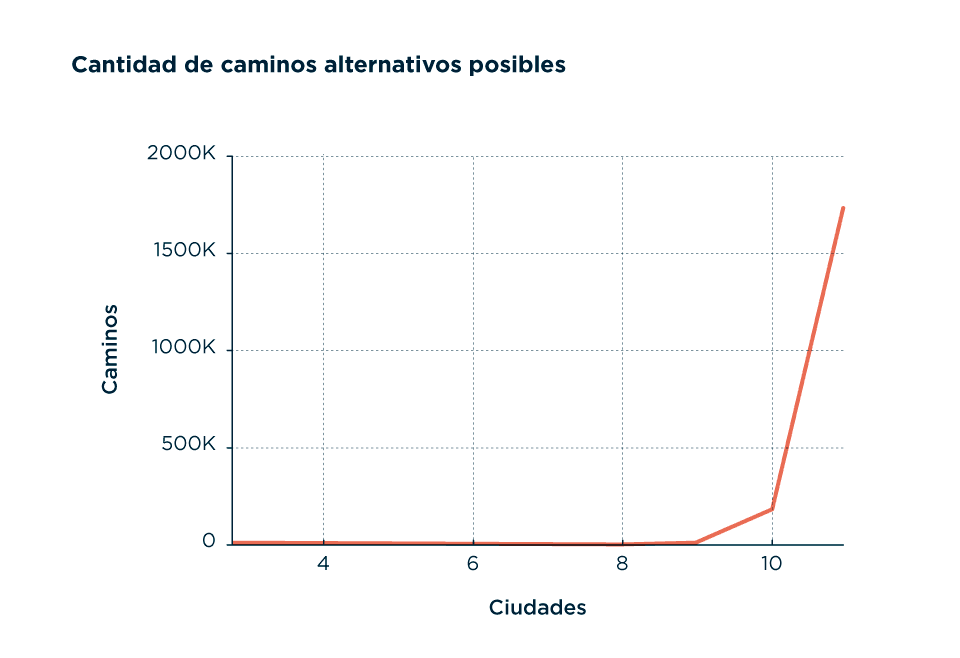
Podemos ver cómo la cantidad de combinaciones despega de golpe y entra en modo ‘al infinito y más allá’, complicándole la vida a cualquiera, pero al mismo tiempo ofreciéndole el problema de una carrera académica completa a múltiples investigadores especializados en problemas de optimización.
El problema del viajante es tan imponente que es en sí mismo parte de la historia de la computación, y cada vez que alguien encuentra una aproximación atractiva hay un mundillo atento e interesado, pero no es un problema novedoso si lo pensamos desde una perspectiva más amplia. ‘Cómo unir múltiples puntos de manera de aprovechar recursos en todos’ es una situación tan común que tiene más que ver con la vida que con la computación, o, por lo menos, una pregunta que nos muestra que la vida puede ser vista como un caso particular de la computación. ¿Qué es lo apto en la supervivencia del más apto sino el aprovechamiento de recursos para la supervivencia y expansión del acervo genético?
Si bien el concepto de redes es central y útil para pensar este problema, entender los caminos que recorremos en el presente como redes aisladas de su historia es despreciar datos de ese trayecto en particular que pueden ser informativos para entender las estructuras presentes. Porque da la impresión de que todo surge de un gran plan cuando, en realidad, en la práctica, los caminos que recorremos son el resultado de años y años de evolución, de la inclusión de tecnologías que, a medida que se incorporan, nos obligan a reformar esas estructuras, a repensarlas. A desarmar y desandar tramos que antes eran significativos pero que hoy dejaron de serlo. Basta ver cómo una ruta de avión nueva afecta el tránsito entre dos ciudades para entender que una red de transporte está integrada a su propia historia y no es puro presente.
Nuestras redes modernas de transporte se basan en la emergencia de caminos durante milenios. Al principio teníamos sólo caminos prehistóricos, del mesolítico, conformados de pisadas de humanos buscando unir asentamientos o geografías ricas en recursos, hechas a fuerza de prueba y error o basadas en los caminos elegidos por los animales (mediante procesos similares de prueba y error). Mucho después vendrían desarrollos orientados por las ciudades, desde los puestos del 1700 dando lugar a carreteras para carruajes, primero de una vía, después de dos, creciendo eventualmente hasta generar autopistas y redes ferroviarias. Pero el camino de los caminos siempre cae en las mismas preguntas: ¿son estos caminos eficientes? Si los hiciéramos hoy desde cero, ¿serían parecidos? ¿Cómo podemos pensarlos para ser eficientes en términos de costo, pero al mismo tiempo resilientes a la falla? Podemos reunir ingenieras, diseñadores urbanos y de redes de transporte, matemáticas y computólogos. O podemos tirar un hongo y verlo crecer.
*02/07/2018 NOTA DEL AUTOR: este es el primer punto (de muchos) donde se usa la palabra ‘hongo’. ESTÁ MAL, o pòr lo menos es un gran ‘es más complicado‘. Un montón de gracias a los micólogos que me avisaron.
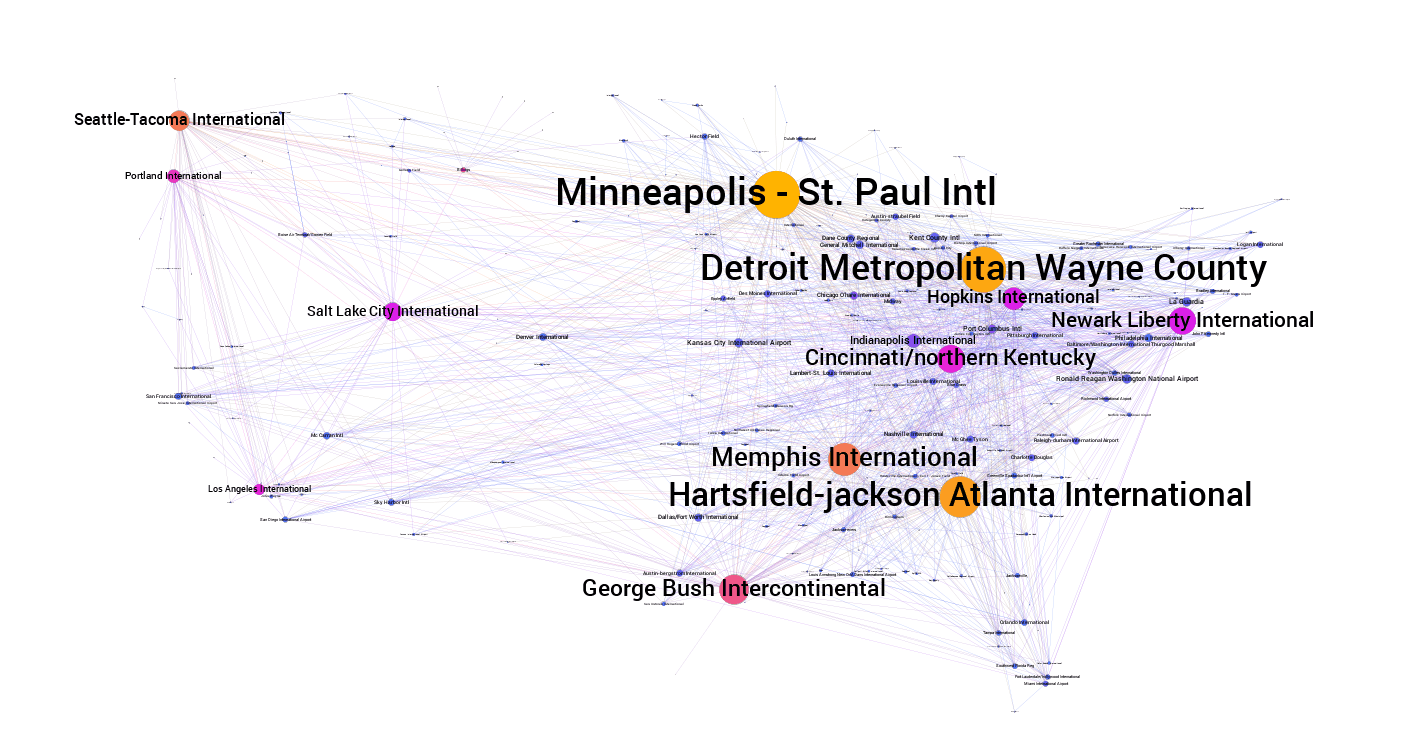
Grafo de los aeropuertos de EE.UU. pintados por centralidad (gradiente que va de amarillo para el más central a violeta para los menos), dispuestos en el espacio por latitud y longitud, para que quede precioso y dibuje un mapa territorial, además de generar cierta tensión con lo de ‘podemos tirar un hongo y verlo crecer’.
La necesidad de aproximarse al problema de unir todos estos puntos de manera eficiente tomó un giro hermoso e inesperado a medida que fuimos entendiendo que no era un problema sólo de los humanos. Y si alguien está pensando en hormigas, mejor, porque yo también. En 1997, Marco Dorigo escribió un método que genera soluciones aproximadas ‘bastante buenas’ para el problema del viajante, usando una simulación de una colonia de hormigas a la que llamó ACS (Ant Colony System) en un ejercicio de simplicidad que agradeceremos por siempre. Este modelo imita el comportamiento observado en las hormigas reales de encontrar caminos cortos entre las fuentes de comida y su nido, los que emergen como un comportamiento la preferencia de cada hormiga de seguir el sendero de feromonas depositado por las otras hormigas.

Cada hormiga recorre un camino y deja un rastro de feromonas que le da información a la que sigue.
Pero si bien la hormiga (o, estrictamente, el hormiguero) como método de aproximación computacional no tradicional al problema del viajante es de lo más divertido, no es práctico. Lo ideal, si queremos realmente aprovechar un organismo vivo para aproximar soluciones a este tipo de problemas, sería tener un organismo amigable para el laboratorio. Una versión equivalente a los modelos de laboratorio tradicionales como el ratón, la planta Arabidopsis o el gusano C. elegans, pero capaz de atacar estos problemas. Acá es donde entra en acción Physarum plasmodium.
Moho mucilaginoso, conocido por crecer casi en cualquier lado oscuro y húmedo, Physarium crece como un protoplasma con múltiples núcleos que forman una estructura de tubos de distintos diámetros por los que fluye ese protoplasma, formando un organismo distinto de la suma simple de sus núcleos: un sincicio, donde no hay división entre células. O sea, no hay células (o hay una, enorme). Pero lo más interesante de Pepe (P. p, je) es lo que pasa cuando se lo pone a resolver un problema de transporte. Cuando enfrentan a Pepe con un laberinto detrás del cual hay comida, este inmediatamente crece en todas las direcciones, pero a medida que pasa el tiempo, uno y sólo uno de los caminos de ese laberinto se ve ocupado por una vía principal de comunicación entre la entrada (que tiene una fuente de alimento) y la salida (que también la tiene). Este camino principal va ganando grosor hasta que toda la estructura del hongo ocupa solamente este trayecto: la (mejor) solución al laberinto. De manera ciega, tanteando primero al azar y después reforzándose por retroalimentación positiva, Physarium establece un vínculo eficiente en una forma que no quiero llamar inteligente, pero que me cuesta mucho descartar como tal, al punto que más bien preferiría hacer un recorte de lo que inteligente significa, y decir que, a su manera, este sistema ha intercambiado información con el exterior, la ha procesado y se ha adaptado al entorno de una manera de lo más piola.
Pero la potencia de este chiquilín de ninguna manera termina acá. Así como puede unir dos puntos eficientemente, se impone la pregunta de si puede unir más. Así es que un grupo de investigadores decidió presentarle un desafío: vamos a poner una plaquita de petri (medio de cultivo donde puede crecer el moho) con comida en lugares que imitan la posición geográfica de centros urbanos alrededor de Tokio y ver cómo conecta esos puntos.

Podemos ver cómo Physarium diseña, sin diseñar, una red de transporte. También podemos ver lo difícil que es diferenciar un experimento que sale bien de un yogur olvidado.
El resultado fue ‘las rutas que se forman son sorprendentemente parecidas a las que diseñamos durante años gracias al trabajo de un montón de gente especializadísima’. Pero los investigadores no se quedaron con este ya interesante y hermoso resultado, sino que se hicieron otras preguntas. Dado que para diseñar una red de transporte tenemos que tener en cuenta condiciones del terreno, como pueden ser la altura de las montañas o que no se puede construir sobre el mar, ¿podemos dar de alguna manera esas señales de dificultad y ver qué pasa con el crecimiento de Physarium?
Como Pepe es un moho, la luz tiende a no ser el mejor amigo de nuestro ingeniero, así que decidieron que a medida que el terreno fuese más alto iban a exponerlo a más luz, para simular esa dificultad. Lo que pasó a continuación no sorprende a nadie, porque medio que es el hilo de la nota, pero seguro puso muy contentos a los investigadores: mientras más se parecían las condiciones a las reales, más se parecía la red de Physarium al sistema de trenes que conecta esos puntos.
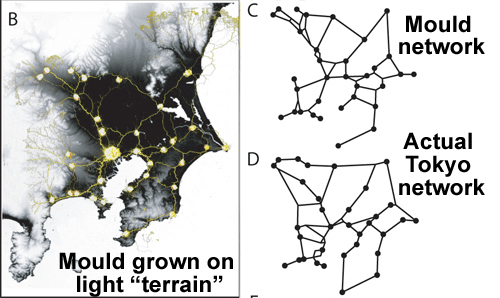
– Pe…pero. Yo pasé 10 años estudiando ingeniería y optimización. – Y yo tengo 4 mil millones de años de selección natural de hacer esto, no vengas a chapear antigüedad.
Incluso se pudieron observar parámetros como qué tan eficiente es la red o qué tan resiliente resulta al perder un nodo (algo que podemos imaginar como ‘se inundó la estación de tren’ de determinada ciudad/nodo, en términos de red de transporte o ‘me comen un pedazo’ si sos un hongo), y siempre el hongo daba resultados similares a los de la red diseñada por humanos. Como ‘hecho el in vivo, soñado el in silico’, otro grupo de investigadores armó un modelo computacional que imitaba esta idea del hongo de ‘crezco para todos lados, pero una vez que encuentro comida, esa señal retroalimenta los caminos que la incluyen y los engrosan un poquito, lo que hace que transporte más comida, lo que hace que se engrosen’, logrando que la realidad que supere a la realidad que supere a la ficción supere a la ficción. EMOJI PENSATIVO
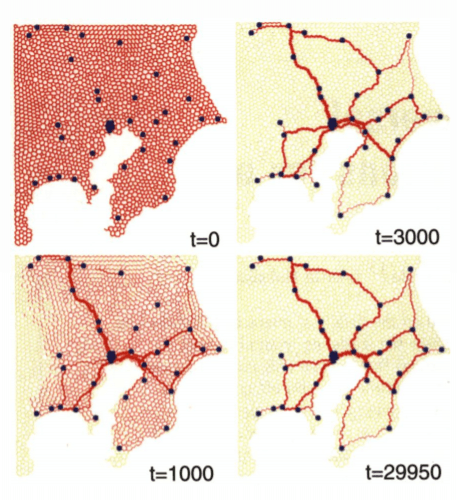
Así luce un hongo simulado a lo largo del tiempo.
Como ya estábamos todos en el baile y locos por los mohos, otro otro grupo de investigadores apenas unos años después decidió modelar los sistemas de transporte terrestre para 12 regiones del mundo: África, Australia, Bélgica, Brasil, Canadá, China, Alemania, España + Portugal, Italia, Malasia, México, Holanda, Gran Bretaña y los Estados Unidos. Para eso, pusieron pedacitos de avena en las ‘ciudades’ principales de cada unos de esos territorios y dejaron a Physarium crecer a partir de la ciudad más grande, hasta que se estabilizara y formara la red completa.
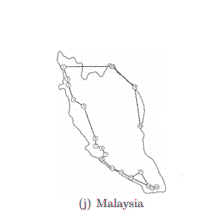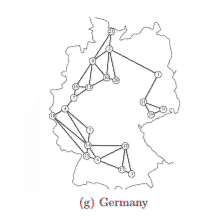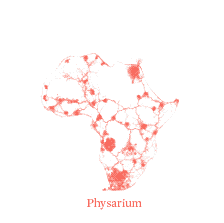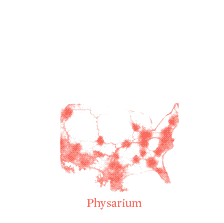
Una y otra y otra vez, Physarium generaba rutas que eran comparables en términos de eficiencia con las diseñadas por humanos, siendo algunas como Italia, Malasia o Canadá extremadamente parecidas (0.85, 0.76 y 0.67 de superposición, respectivamente). Una red optimizada por miles de millones de años de evolución para encontrar el punto exacto de equilibrio entre redundancia, eficiencia y resiliencia que favorece la supervivencia del más ingeniero.

Ya fue todo, traigan una impresora 3D, simulemos las montañas de Alemania y pongamos el hongo a crecer acá.
Este trabajo llamó tanto la atención que, tomando como modelo la forma de crecimiento de Physarium, y aplicándolo a resolver el problema del viajante, Jeff Jones and Andrew Adamatzky simularon un ingeniero moho virtual que es capaz de resolver el problema de manera más que adecuada (con caminos de entre un 4 y un 10% más largos que la mejor solución posible), de una manera completamente distinta de las que se habían usado hasta el momento.
Computación inspirada en la biología, o computación inspirada en la computación, para resolver problemas reales, tangibles, complejos. Problemas para los cuales puede que no necesitemos soluciones perfectas, sino soluciones lo suficientemente buenas, y accesibles en tiempos alcanzables. Aproximaciones novedosas basadas en organismos que vienen solucionándolo, sin querer queriendo, desde siempre. Tranquilidad, sobre todas las cosas, al saber que la próxima vez que me pregunten por problemas como estos voy a tener una historia para contar, pero más que nada la seguridad de que la próxima vez que entre en una habitación llena de gente, que me enfrente a la tensión de recorrer ese territorio, de completar ese grafo, de saludar a uno por uno, voy a poder hacerlo de la manera que corresponde: dándole un pedacito de avena a cada quien, untándolos con Physarium, poniéndolos en la oscuridad, esperando que la red se estabilice y dejando que el hongo me guíe.

